BOJ_11444_피보나치수6_JAVA
문제 : 피보나치 수 6
링크 : BOJ_11444_피보나치수6
접근 방식
피보나치 수를 행렬을 통해서도 구할 수 있다는 사실을 아는가? 나는 몰랐다.
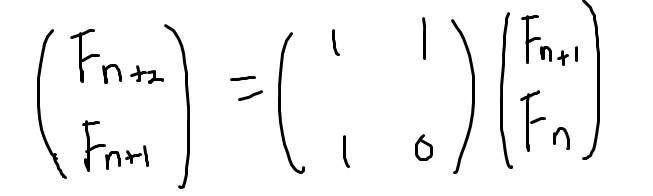
피보나치 수를 구하는 식을 행렬로 나타내면 다음과 같고,
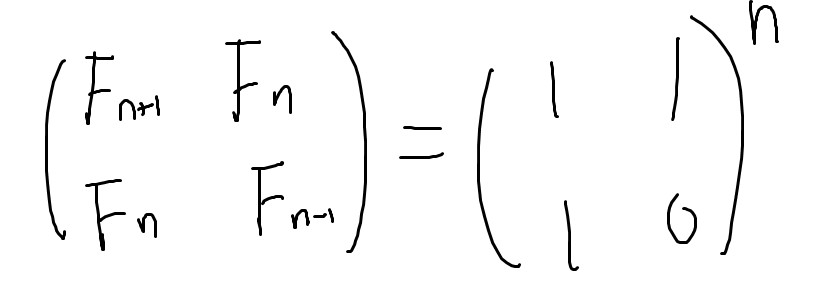
이 식을 정리하면 위와 같이 나타낼 수 있다고 한다.
행렬의 제곱, 뭔가 익숙한 것이 어제 풀었던 내용을 응용하면 될 것 같다.
풀이 방법
-
N은 int 값의 범위를 넘는 값을 담아야 하기 때문에 long으로 생성해 값을 읽어온다.
-
2*2 배열을 선언하고 순서대로 1,1,1,0을 할당해준다.
-
분할정복을 이용한 행렬의 제곱 함수를 이용하여 2*2배열의 N제곱을 구하여 새로운 배열을 생성하여 할당한다.
-
구한 행렬의 (0,1)의 값을 출력한다.
행렬을 제곱하는 함수에 대해서는 이쪽 글을 참고하면 된다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class BOJ_11444_피보나치수6 {
static final int NUM = 1000000007;
static final int N = 2;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
long N = Long.parseLong(in.readLine());
long arr[][] = new long[2][2];
arr[0][0] = 1;
arr[0][1] = 1;
arr[1][0] = 1;
arr[1][1] = 0;
// N번째 수는 위 행렬의 n제곱의 0,1번째 수
long ans[][] = fpow(arr, N);
System.out.println(ans[0][1]);
}
static long[][] fpow(long[][] c, long n) {
if(n == 1) {
return c;
}else {
long[][] x = fpow(c, n/2);
long[][] temp = new long[N][N];
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
for(int k=0;k<N;k++) {
temp[i][j] += x[i][k] * x[k][j];
}
temp[i][j] %= NUM;
}
}
if(n%2 == 0) {
return temp;
}else {
long temp2[][] = new long[N][N];
for(int i=0;i<N;i++) {
for(int j=0;j<N;j++) {
for(int k=0;k<N;k++) {
temp2[i][j] += temp[i][k] * c[k][j];
}
temp2[i][j] %= NUM;
}
}
return temp2;
}
}
}
}