BOJ_1707_이분그래프_JAVA
문제 : 이분그래프
링크 : BOJ_1707_이분그래프
접근 방식
그래프를 탐색하여 이분그래프인지 아닌지 조사해야 하는 문제이다. 이 문제를 풀려면 먼저 이분그래프의 정의에 대해 알아야 할 필요가 있다. 문제의 설명에서는 그래프의 정점의 집합을 둘로 분할했을 때, 각 집합에 속한 정점끼리는 서로 연결되지 않도록 분할할 수 있는 상태를 이분그래프라고 한다고 적혀있다. 이분그래프에는 많은 종류가 있지만 그 중 하나를 가져와보겠다.
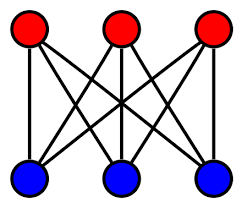
위 그림에서 빨간 정점과 파란 정점은 간선을 가지고 있다. 하지만 빨간 점 사이, 파란 점 사이 끼리는 간선이 존재하지 않는다.
그렇다면 임의의 그래프가 주어졌을 때 이분그래프인지 어떻게 알 수 있을까? 그 방법은 DFS로도 알 수 있고, BFS로도 구할 수 있다.
DFS를 통해 구한다면, 탐색할 때마다 색을 2개로 나눠 서로 다르게 부여하며 앞으로 방문할 지역이 이미 방문한 지역이면서 이전 노드와 같은 색이라면 이분그래프가 아닌 것이고, 모든 탐색을 마치는 동안 위와 같은 경우가 발생하지 않았다면 이분그래프이다.
BFS를 통해 구한다면, 큐에 삽입할 때마다 Level이 증가되는 것을 이용하여 직전 레벨의 부여된 색과 현재 레벨의 색이 같다면 이분그래프가 아니다. 역시 BFS 탐색이 모두 끝나는 동안 위와 같은 경우가 발생하지 않았다면 이분그래프이다.
여기서는 BFS로 풀어보겠다.
풀이 방법
-
테스트 케이스 만큼 반복한다.
-
주어지는 입력값이 간선정보로 주어지기 떄문에, Node 클래스를 만들어 인접리스트 형태로 구현했다. 멤버변수로, 자신의 정점 정보를 저장할 int형 변수와 같은 정점의 다음 간선을 저장할 Node형 변수가 있다.
-
간선 정보를 저장할 배열, 정점의 개수, 간선의 개수를 저장할 변수를 생성하고, 입력값으로부터 읽어들여 각각 저장한다. 나는 한참을 해멨는데, 따로 방향이 있다는 얘기가 없어서 무향 그래프인 것 같다. 그렇기 때문에 예를 들어 1 3으로 입력값이 들어온다면, 1-3 간선과 3-1을 같이 처리해줘야한다.
-
이후 BFS 탐색을 수행한다.
-
BFS 메서드의 인자값으로는 방문여부 + 색을 부여할 int형 배열을 받는다.
-
정점의 정보를 저장할 큐를 생성한다. 이후 1부터 V까지 반복한다. (위 반복을 하는 이유는 이후에 설명하겠다.) ~ 9 까지
-
만약 현재 정점이 아직 방문하지 않은 상태(=0인 상태)라면 현재 정점에 1을 부여하고 해당 정점 번호를 queue에 추가한다.(초기값 할당)
-
BFS 탐색 과정을 거친다. 각 노드별 인접리스트로 생성되어있는 간선을 모두 불러와 현재 정점의 색과 비교하여, 같은 색이라면 “NO”를 반환한다.
-
만약 간선과 연결되어있는 정점이 아직 방문하지 않았다면, 현재의 색의 반대되는 색을 부여하고 큐에 해당 정점 번호를 추가한다. (1이라면 2를, 2라면 1을 부여)
-
모든 반복이 종료되었는데 반환되지 않았다면, “YES”를 반환한다.
-
5번에서, 1~V까지 반복한 이유에 대해서 설명하겠다. 그래프의 모든 정점이 연결되어있다면, 탐색을 할 때 임의의 1개의 시작점만 정해도 모든 노드가 탐색이 가능하다. 하지만, 그래프의 정점이 모두 연결 되어있지 않고 단절 되어있는 경우에는 임의의 1개의 정점만으로 모두 탐색을 했다고 할 수 없다. 그렇기 때문에 모든 정점에 대해서 BFS 탐색을 진행하는 것이다. 그 중 이미 방문처리 되어있는 노드는, 다른 노드를 시작점으로 탐색했을 때 그 노드와 연결이 되어있는 것으로 생각할 수 있다.
-
반환된 값을 출력한다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
class Node {
int num;
Node link;
public Node(int num, Node link) {
super();
this.num = num;
this.link = link;
}
@Override
public String toString() {
return "Node [num=" + num + ", link=" + link + "]";
}
}
public class BOJ_1707_이분그래프 {
// BFS로 풀어보기
static int V, E;
static Node[] nodes;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(in.readLine());
for (int tc = 0; tc < T; tc++) {
StringTokenizer st = new StringTokenizer(in.readLine(), " ");
V = Integer.parseInt(st.nextToken());
nodes = new Node[V + 1];
E = Integer.parseInt(st.nextToken());
for (int i = 0; i < E; i++) {
st = new StringTokenizer(in.readLine(), " ");
int n = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
nodes[n] = new Node(to, nodes[n]);
nodes[to] = new Node(n,nodes[to]);
}
System.out.println(bfs(new int[V + 1]));
}
}
static String bfs(int[] visited) {
Queue<Integer> queue = new LinkedList<>();
// 1, 2 = 2분 구분하는 수
for (int i = 1; i <= V; i++) {
if (visited[i] == 0) {
visited[i] = 1;
queue.add(i);
}
while (!queue.isEmpty()) {
int current = queue.poll();
for (Node temp = nodes[current]; temp != null; temp = temp.link) {
if (visited[temp.num] == visited[current]) {
return "NO";
}
if (visited[temp.num] == 0) {
if (visited[current] == 1) {
visited[temp.num] = 2;
} else {
visited[temp.num] = 1;
}
queue.offer(temp.num);
}
}
}
}
return "YES";
}
}