BOJ_2304_창고다각형_JAVA
문제 : 창고다각형
링크 : BOJ_2304_창고다각형
접근 방식
이 문제는 내가 어렵게 푼 건 지는 잘 모르겠지만, 느끼기에 매우 복잡한 문제였다.
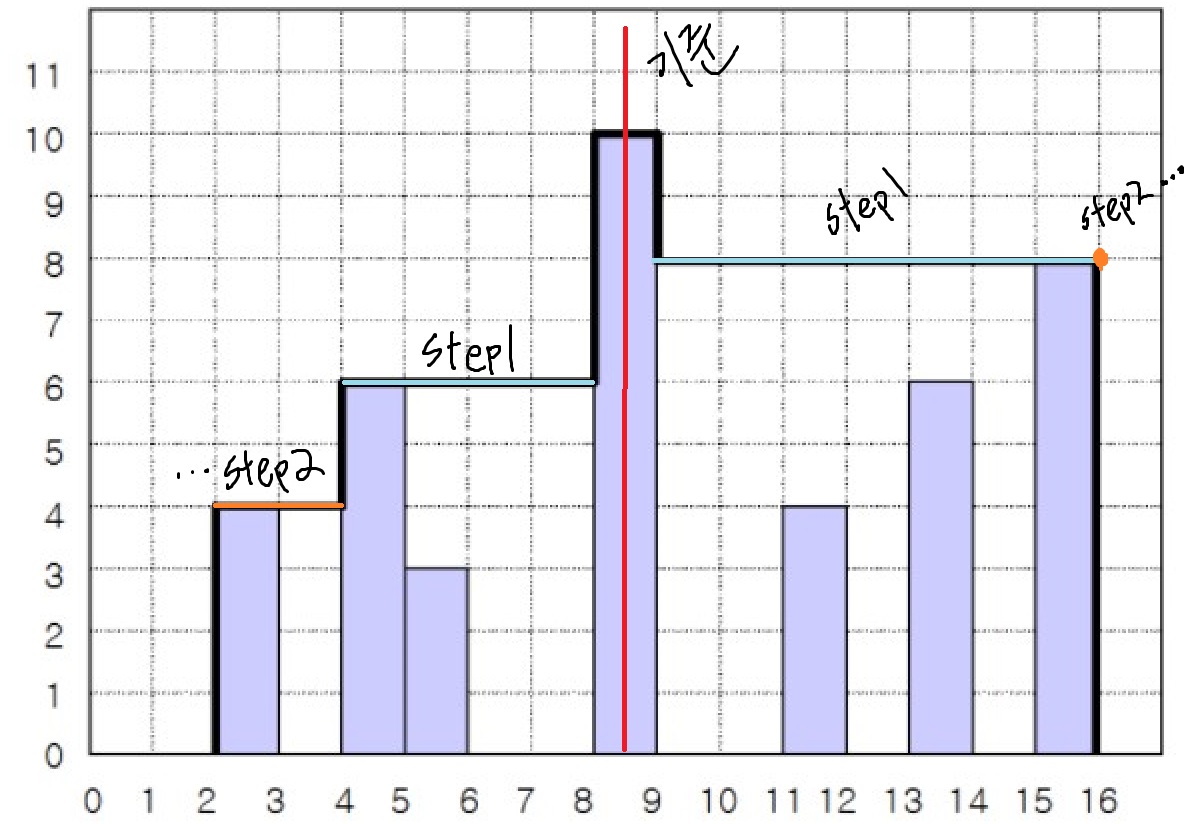
먼저, 순서가 뒤죽박죽으로 주어지는 기둥의 값을 위치를 기반으로 정렬하여 위 사진처럼 만들어줘야한다.
그 후, 가장 긴 막대를 찾아 넓이를 구하고 그 막대를 기준으로 양쪽으로 탐색을 한다.
막대 기준 오른쪽에서 가장 긴 막대, 왼쪽에서 가장 긴 막대를 하나씩 찾아서, 각 위치의 차와 높이를 이용해 넓이를 구하는게 그림에 표현한 1Step이다. 그 후, 양쪽에 찾아낸 막대를 또 하나의 기준으로 잡아, 각각의 왼쪽, 오른쪽에서 가장 긴 막대를 찾아서 다시 한 번 넓이를 구하는 것이 2Step이다.
이 작업을 양 끝 막대에 다다르기까지 반복하여 구해진 넓이를 모두 더하면 창고다각형의 넓이를 구할 수 있다. 소스코드에 적힌 주석을 참고하여 코드를 보면 도움이 될 수도 있다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;
public class BOJ_2304_창고다각형 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
// 값 읽어와서 정수로 형변환 저장
int N = Integer.parseInt(in.readLine());
// 정수형 배열 리스트 선언 및 생성
List<Integer[]> list = new ArrayList<>();
// StringTokenizer 선언
StringTokenizer st;
// 값 할당 과정
// N 번만큼 반복
for (int i = 0; i < N; i++) {
// 값 읽어와서 StringTokenizer로 저장
st = new StringTokenizer(in.readLine(), " ");
// Integer 1차원 배열로 생성, 입력값을 각각 집어넣는다. 저장 배열의 크기는 2이다.
Integer[] temp = new Integer[2];
// 기둥의 위치
temp[0] = Integer.parseInt(st.nextToken());
// 기둥의 높이
temp[1] = Integer.parseInt(st.nextToken());
// Integer 1차원배열을 리스트에 추가한다.
list.add(temp);
}
// 정렬을 하는데, 기둥의 위치(list(i)의 0번)을 기준으로 정렬한다. 람다식 이용
Collections.sort(list, (o1, o2) -> {
if (o1[0] >= o2[0]) {
return 1;
} else {
return -1;
}
});
// X는 오른쪽 리스트를 탐색할 변수
int X = 0;
// Y는 왼쪽 리스트를 탐색할 변수
int Y = 0;
// H는 높이이다.
int H = 0;
// 리스트의 길이만큼 반복
for (int i = 0; i < list.size(); i++) {
// 높이가 최댓값인 수를 구하는 조건문이다.
if (H <= list.get(i)[1]) {
// X,Y에 리스트 인덱스 저장(최댓값일 경우)
X = i;
Y = i;
// 높이가 최대일 때 해당 높이 저장
H = list.get(i)[1];
}
}
// 창고다각형의 넓이를 저장할 변수, 총 넓이를 해당 변수에 계속 더해준다.
int ans = 0;
// 가장 높은 기둥일 때의 넓이를 먼저 저장.
ans += list.get(X)[1];
// 오른쪽 탐색
while (true) {
// 가장 높은 기둥의 오른쪽을 탐색하는데, 2번째로 높은 기둥의 높이를 저장할 변수
int inH = 0;
// 2번째로 높은 기둥의 인덱스를 저장할 변수
int x = 0;
// 멈추는 조건
// 만약 가장 높은 기둥 오른쪽에 기둥이 없다면 반복문을 종료한다.
if (X + 1 >= list.size()) {
break;
}
// X+1인 이유, 가장 높은 기둥의 다음 기둥부터 비교하기 위함.
// X+1부터 list의 사이즈-1까지 반복한다.
for (int i = X + 1; i < list.size(); i++) {
// 오른쪽에 있는 기둥 중 최댓값을 구하는 조건문
if (list.get(i)[1] > inH) {
// 최댓값의 높이와
inH = list.get(i)[1];
// 최댓값일 때의 기둥의 인덱스를 저장
x = i;
}
}
// 2번째로 높은 기둥의 인덱스를 구했다.
// 오른쪽의 기둥은 가장 높은 기둥보다 위치값이 더 크므로,
// (2번째로 높은 기둥의 위치 - 가장 높은 기둥의 위치)*2번째로 높은 기둥의 높이
// 위 계산식으로 넓이를 구하여 총 넓이에 더해준다.
ans += (list.get(x)[0] - list.get(X)[0]) * list.get(x)[1];
// 2번째로 높은 기둥을 찾았다면, 그 기둥을 기준으로 오른쪽에 다시한 번 더 낮은 기둥이 있는지 찾아봐야한다.
// 2번째로 높은 기둥을 가장 높은 기둥으로 기준삼아 다시 반복해준다.
X = x;
}
// 왼쪽 탐색 : 오른쪽과 동일한 로직으로 이루어지지만 세부적으로 조금 다르다.
while (true) {
// 가장 높은 기둥의 왼쪽을 탐색하는데, 2번쨰로 높은 기둥의 높이를 저장할 변수
int inH = 0;
// 2번째로 높은 기둥의 인덱스를 저장할 변수
int y = 0;
// 만약 가장 높은 기둥 왼쪽에 기둥이 없다면 반복을 종료한다.
if (Y - 1 < 0) {
break;
}
// Y-1부터 시작하는 이유, 가장 높은 기둥의 이전 기둥부터 비교하기 위함.
for (int i = Y - 1; i >= 0; i--) {
// 왼쪽에 있는 기둥 중 최댓값을 구하는 조건문
if (list.get(i)[1] > inH) {
// 최댓값의 높이와
inH = list.get(i)[1];
// 최댓값일 때의 기둥의 인덱스를 저장
y = i;
}
}
// 2번째로 높은 기둥의 인덱스를 구했다.
// 왼쪽의 기둥은 가장 높은 기둥보다 위치값이 더 작으므로,
// (가장 높은 기둥의 위치 - 2번째로 높은 기둥의 위치)*2번째로 높은 기둥의 높이
// 위 계산식으로 넓이를 구하여 총 넓이에 더해준다.
ans += (list.get(Y)[0] - list.get(y)[0]) * list.get(y)[1];
// 2번째로 높은 기둥을 찾았다면, 그 기둥을 기준으로 왼쪽에 다시 한 번 더 낮은 기둥이 있는지 찾아봐야한다.
// 2번째로 높은 기둥을 가장 높은 기둥으로 기준삼아 다시 반복해준다.
Y = y;
}
// 모두 더해진 넓이를 출력한다.
System.out.println(ans);
}
}