BOJ_2564_경비원_JAVA
문제 : 경비원
링크 : BOJ_2564_경비원
접근 방식
문제를 읽으면서는 크게 감이 안 잡혔다. 그림을 기준으로 수를 구분해봤을 때, 문제를 풀 실마리가 생각났다.
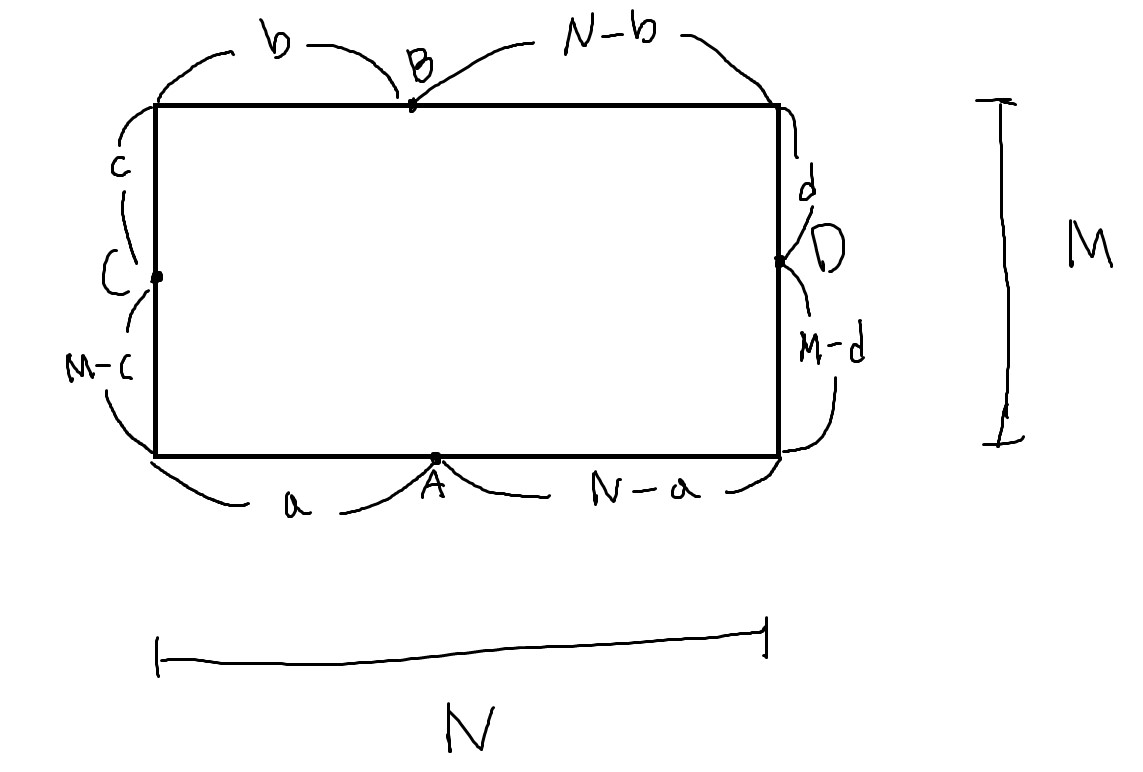
N*M 넓이의 사각형 위의 4개의 점(대문자)과 그 길이(소문자)라고 할 때, 반대편의 길이는 가로, 세로 길이에서 각각의 길이만큼 뺀 값이다. 매우 간단한 상식이다. 경비원의 문제를 보고 이 사실을 이용하여 식을 만들었다.
-
동근이 동일때 (4) - 상점이 동 : 상점 - 동근 절댓값 - 상점이 서 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점) - 상점이 남 : M - 동근 + 상점 - 상점이 북 : 동근 + N - 상점
-
동근이 서일때 (3) - 상점이 동 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점) - 상점이 서 : 상점 - 동근 절댓값 - 상점이 남 : M - 동근 + 상점거리 - 상점이 북 : 동근 + 상점
-
동근이 남일때 (2) - 상점이 동 : N+M-동근-상점 - 상점이 서 : 동근 + M - 상점 - 상점이 남 : 상점 - 동근 절댓값 - 상점이 북 : Min(M + 동근 + 상점, 2N + M -동근 - 상점)
-
동근이 북일때 (1) - 상점이 동 : N - 동근 + 상점 - 상점이 서 : 동근 + 상점 - 상점이 남 : Min(M + 동근 + 상점, 2N + M -동근 - 상점) - 상점이 북 : 동근 - 상점 절댓값
풀이 방법
-
입력값을 읽어들여 상점의 위치와 방향 정보를 2차원 배열로 저장한다. 동근이의 위치, 방향은 따로 저장해둔다.
-
접근 방식 칸에 적은 규칙대로 Switch문을 만든다.
-
각 조건에 따라서 상점의 방향, 위치별 해당 조건에 맞는 수식을 계산한다.
-
수식을 통해 구해진 최소 거리를 모두 더하여 출력한다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BOJ_2564_경비원 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int R = Integer.parseInt(in.readLine());
int[][] arr = new int[R][2];
for (int i = 0; i < R; i++) {
st = new StringTokenizer(in.readLine(), " ");
for (int j = 0; j < 2; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
st = new StringTokenizer(in.readLine(), " ");
// 동근이 방향
int dongDir = Integer.parseInt(st.nextToken());
// 동근이 거리
int dongDis = Integer.parseInt(st.nextToken());
/*
총정리
/*
1. 동근이 동일때 (4)
- 상점이 동 : 상점 - 동근 절댓값
- 상점이 서 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점)
- 상점이 남 : M - 동근 + 상점
- 상점이 북 : 동근 + N - 상점
2. 동근이 서일때 (3)
- 상점이 동 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점)
- 상점이 서 : 상점 - 동근 절댓값
- 상점이 남 : M - 동근 + 상점거리
- 상점이 북 : 동근 + 상점
3. 동근이 남일때 (2)
- 상점이 동 : N+M-동근-상점
- 상점이 서 : 동근 + M - 상점
- 상점이 남 : 상점 - 동근 절댓값
- 상점이 북 : Min(M + 동근 + 상점, 2N + M -동근 - 상점)
3. 동근이 북일때 (1)
- 상점이 동 : N - 동근 + 상점
- 상점이 서 : 동근 + 상점
- 상점이 남 : Min(M + 동근 + 상점, 2N + M -동근 - 상점)
- 상점이 북 : 동근 - 상점 절댓값
*/
int ans = 0;
int sum = 0;
for (int i = 0; i < R; i++) {
int shopDir = arr[i][0];
int shopDis = arr[i][1];
// 동근이 위치 기반 스위치문
switch (dongDir) {
// 동근이 동
case 4:
// 상점 위치 기반 스위치문
switch (shopDir) {
// 상점 동 : 상점 - 동근 절댓값
case 4:
ans = Math.abs(shopDis - dongDis);
break;
// 상점 서 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점)
case 3:
ans = Math.min(N+dongDis+shopDis, 2*M+N-dongDis-shopDis);
break;
// 상점 남 : M - 동근 + 상점
case 2:
ans = M - dongDis + shopDis;
break;
// 상점 북 : 동근 + N - 상점
case 1:
ans = dongDis + N - shopDis;
break;
}
break;
// 동근이 서
case 3:
switch (shopDir) {
// 상점이 동 : Min(N + 동근 + 상점, 2M + N - 동근 - 상점)
case 4:
ans = Math.min(N+dongDis+shopDis, 2*M+N-dongDis-shopDis);
break;
// 상점 서 : 상점 - 동근 절댓값
case 3:
ans = Math.abs(shopDis - dongDis);
break;
// 상점 남 : M - 동근 + 상점거리
case 2:
ans = M - dongDis + shopDis;
break;
// 상점 북 : 동근 + 상점
case 1:
ans = dongDis + shopDis;
break;
}
break;
// 동근이 남
case 2:
switch (shopDir) {
// 상점 동 : N+M-동근-상점
case 4:
ans = N + M - dongDis - shopDis;
break;
// 상점 서 : 동근 + M - 상점
case 3:
ans = dongDis + M - shopDis;
break;
// 상점 남 : 상점 - 동근 절댓값
case 2:
ans = Math.abs(shopDis - dongDis);
break;
// 상점 북 : Min(M + 동근 + 상점, 2N + M -동근 - 상점)
case 1:
ans = Math.min(M+dongDis+shopDis, 2*N + M - dongDis-shopDis);
break;
}
break;
// 동근이 북
case 1:
switch (shopDir) {
// 상점 동 : N - 동근 + 상점
case 4:
ans = N - dongDis + shopDis;
break;
// 상점 서 : 동근 + 상점
case 3:
ans = dongDis + shopDis;
break;
// 상점 남 : Min(M + 동근 + 상점, 2N + M -동근 - 상점)
case 2:
ans = Math.min(M+dongDis+shopDis, 2*N + M - dongDis-shopDis);
break;
// 상점 북 : 동근 - 상점 절댓값
case 1:
ans = Math.abs(shopDis - dongDis);
break;
}
break;
}
sum = sum + ans;
}
System.out.println(sum);
}
}