문제 : 최대공약수와 최소공배수

링크 : BOJ_2609_최대공약수와 최소공배수

접근 방식

학과 과정 중, 유클리드 알고리즘에 대해 배운 적이 있다. 그 당시에 나름 열심히 수업을 들었는데, 이 문제를 보면서 유클리드 알고리즘이 최대공약수를 구하는 알고리즘이라는 것만 기억나고 아무 것도 생각이 나지 않았다.

유클리드 알고리즘이란, 최대공약수를 구하는 알고리즘이다. 인류 최초의 알고리즘이라고도 한다.

정의는 다음과 같다.

두 양의 정수 a, b(a>b)에 대하여 a = bq + r(0<=r<b)라고 한다면, a,b의 최대공약수는 b,r의 최대공약수와 같다.

즉, gcd(a,b) = gce(b,r)이다.

r이 0이라면, a,b의 최대공약수는 b가 된다.

풀어서 말하면 다음과 같다. a와 b가 있고, a를 b로 나눈 나머지 r이 있다. 여기서 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 것이다.

이것을 최대공약수를 구하는 데 활용해보자.

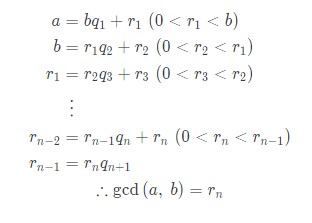
• 출처 : 나무위키 유클리드 호제법 설명 문서

두 양의 정수 a,b에 대해서, 사진처럼 r이 0이 될 때까지 계속해서 이 알고리즘을 반복하면 최종적으로 a, b의 최대 공약수를 구할 수 있다.

그렇다면 이 내용을 자바 코드로 구현해 보았다.

public static int search(int A, int B) {

	while(B != 0) {
		int R = A%B;
		A = B;
		B = R;
	}

	return A;
}

함수명은 임의로 지었다.

1. B가 0이 될 때까지 반복한다.

2. R을 선언해 A%B 연산한 값을 할당한다.(A/B의 나머지)

3. A자리에 B를, B자리에 R을 넣고 위 연산을 반복한다.

4. 최종적으로 B가 0이 되었을 때의 A값이 A,B의 최대공약수이다.

최소공배수는 최대공악수만 구할 수 있다면 매우 쉽게 구할 수 있다.

두 양의 정수 A, B와 A,B의 최대공약수 C가 있다고 할 때.

최소공배수 = A*B/C 이다.

풀이 방법

1. Scanner로 두 입력값을 받아와 A,B에 저장한다.

2. A가 B보다 커야한다는 조건에 대해서 Search 메서드에서 처리할 코드를 작성하지 않았기 떄문에, 받은 A,B 두개의 변수를 비교해 큰 값을 1번 인자값으로, 작은 값을 2번 인자값으로 넣는다.

3. 구해진 최대공약수를 이용해 최소공배수를 계산한다.

4. 최대공약수와 최소공배수를 차례로 출력한다.

소스 코드

import java.util.Scanner;

public class BOJ_2609_최대공약수와최소공배수 {

	public static void main(String[] args) {
		Scanner in = new Scanner(System.in);

		int A = in.nextInt();
		int B = in.nextInt();
		int ans1 =0;
		if(A>B) {
			ans1 = search(A,B);
		}else{
			ans1 = search(B,A);
		}

		int ans2 = A*B/ans1;

		System.out.println(ans1);
		System.out.println(ans2);
}


	public static int search(int A, int B) {

		while(B != 0) {
			int R = A%B;
			A = B;
			B = R;
		}

		return A;
	}

}