BOJ_2579_계단오르기_JAVA
문제 : 정수 삼각형
링크 : BOJ_2579_계단오르기
접근 방식
계단의 시작점부터 도착점까지 얻을 수 있는 최대의 점수를 구해야 하는 문제이다.
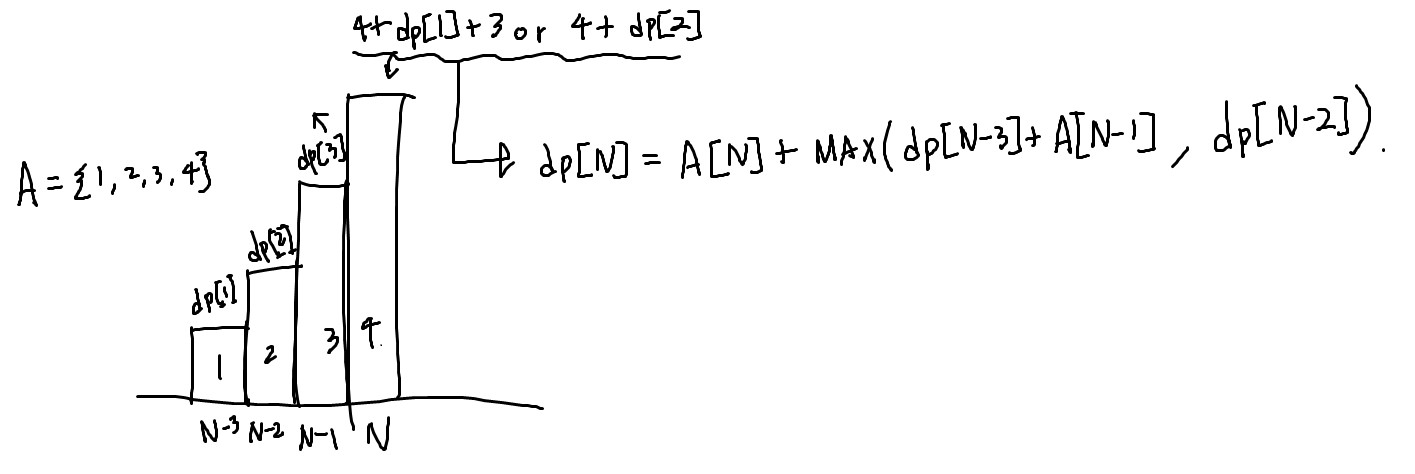
몇 가지 수를 통해 테스트를 했고, 그 결과 다음과 같은 점화식을 구할 수 있었다. DP를 누적된 값으로 정하고, 해당 점화식을 코드로 구현하면 된다.
풀이 방법
-
계단의 개수를 읽어들여 int형 변수 N 에 저장한다.
-
그 이후 N번만큼 반복하며 주어진 값을 읽어들여 N+1 크기의 int형 배열 arr에 저장한다.
-
점화식 dp[N] = arr[N] + Max(dp[N-3]+arr[N-1], dp[N-2]) 는 N이 3 이상이어야 가능하기 때문에 dp[2]까지는 직접 구해서 값을 넣어준다.
-
3부터 N까지 위의 점화식을 반복하여 dp에 값을 저장한다.
-
모든 반복이 끝난 후 dp[N-1]을 출력한다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class BOJ_2579_계단오르기 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(in.readLine());
int[] arr = new int[N+1];
for(int i=0;i<N;i++) {
arr[i] = Integer.parseInt(in.readLine());
}
int[] dp = new int[N+1];
dp[0] = arr[0];
dp[1] = Math.max(arr[0],0)+arr[1];
if(N > 1) {
dp[2] = Math.max(arr[1], dp[0])+arr[2];
}
for(int i=3;i<N;i++) {
dp[i] = Math.max(arr[i-1]+dp[i-3], dp[i-2])+arr[i];
}
System.out.println(dp[N-1]);
}
}