유니티 토막 지식_03
Retr0의 교재를 따르는 실습은 저작권상 앞으로는 짤막하게 한 줄씩만 적도록 하겠다.
오늘은 벡터와 회전에 대해 공부했다. 고등학교 때 배웠던 내용이 조금이나마 떠올라서 조금 그리운 느낌도 들었다.
그렇다고 매 포스팅을 한 줄짜리 일기로 끝낼 수 없기 때문에, 유니티 API 문서를 토대로 유니티를 사용하는데 도움이 되는 지식을 공부하고, 포스팅하려고 한다.
오늘 알아볼 것은 Vector이다.
정의
벡터는 방향과 크기를 설명할 수 있는 기본적인 수학적 개념이다. 게임이나 앱에서 벡터는 종종 캐릭터의 위치, 움직이는 속도, 두 물체 사이의 거리와 같은 기본 특성들을 묘사할 때 사용된다.
벡터 연산은 그래픽스, 물리, 애니매이션 등과 같이 많은 요소에 핵심이 된다. Unity를 최대한 활용하기 위해서는 벡터 연산을 깊이 이해하는게 좋다고 한다.
벡터는 여러 차원으로 표현이 가능하다. Unity는 2D,3D,4D 벡터작업이 가능한 각각의 클래스를 제공한다.
벡터의 연산
덧셈
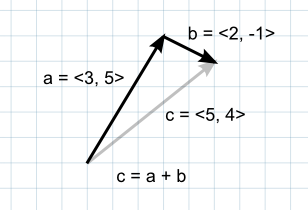
두 벡터의 덧셈은 두 개의 벡터의 좌표를 각각 더해주는 것을 말한다. 좌표를 더하는 순서가 달라지더라도 결과는 같기 때문에 더하는 순서는 상관없다.
벡터가 힘을 나타내는 단위일 때 벡터를 힘의 크기인 강도와 방향으로 간주할 경우 더욱 와닿는다. 두 가지 힘의 벡터를 서로 더하면, 두 힘을 합한 값과 동일한 새로운 벡터가 생성된다. -> 동시에 다수의 서로 다른 컴포넌트에 힘을 가할 때 유용하다. ex) 활을 쏠 때 바람에 따라 세기와 방향이 변동할 수 있음.
그림은 2D Vector로 예시를 들었지만, 3D와 4D에서도 동일하게 적용된다.
뺄셈
벡터의 뺄셈은 특정 오브젝트에서 다른 오브젝트까지의 거리, 방향을 구할 때 주로 사용한다. 이 과정에서 파라미터의 순서는 매우 중요하다.
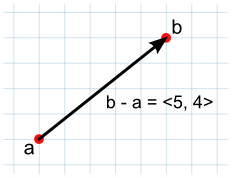
위 그림에서 두 벡터 a, b의 뺄셈 b-a가 의미하는 것은 무엇일까? 바로 a에서 b까지의 거리, 방향 벡터를 의미한다. 물론 반대, a-b는 b에서 a까지의 거리, 방향 벡터이다.
벡터는 값이 아닌 방향이 존재하기 때문에 당연하게도 a-b != b-a이다. 만약 a 위치에서 b위치까지의 거리를 알고싶다면 b의 벡터값에서 a의 벡터값을 뺄셈 해주면 해당하는 거리와 방향의 벡터를 얻을 수 있을 것이다.
벡터의 정규화
정규화된 벡터란, 벡터의 길이가 1인 벡터를 말한다. 정규화 된 벡터를 구하는 방법은 2가지가 있다.
벡터 A가 있다고 할 때
Vector3 A = (1,1,1);
// 벡터의 길이
float distance = A.magnitude;
// 정규화 벡터
Vector3 direction = A / distance;
Vector3 A = (1,1,1);
// 정규화 벡터
Vector3 direction = A.normalized;
스칼라 곱셈과 나눗셈
스칼라는 단순이 크기만을 가지고 있는 것을 말한다. 벡터는 앞서 말했듯 크기, 방향을 함께 가지고 있다.
벡터에 스칼라를 곱한다면 그 결과는 오리지널과 동일한 방향 을 가리키는 벡터이다. 벡터에 스칼라를 곱하거나 나누어도 방향은 변하지 않는다. 그러나 크기는 각각의 벡터의 크기에 해당하는 스칼라를 곱하거나 나눈 값과 같다. 앞의 정규화에서 먼저 사용했는데. A라는 벡터에 A벡터의 크기만큼 스칼라 값을 나눗셈 해주었더니, 크기가 1인 정규화된 벡터가 되었다. 영어로는 normalized Vector라고 한다.
벡터의 내적
벡터의 내적은 두 벡터를 받아 스칼라를 반환한다. 이 스칼라는 두 벡터의 크기를 곱한 후, 그 결과의 두 벡터 사이의 각도에 대해 코사인값을 곱한 것과 같다. 두개의 벡터가 모두 정규화된 벡터일 경우, 코사인 값은 첫 번째 벡터에서 2번째 벡터의 방향으로 기울어진 기울기를 나타낸다. 이 경우 두 벡터의 순서는 상관이 없다. 스칼라는 부호가 없기 때문이다.
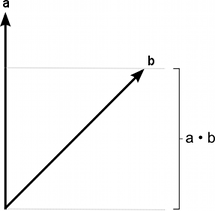
내적은 다른 벡터의 방향에 있는 한 벡터의 크기를 계산 할 때 유용하게 사용할 수 있다. 유니티에서는 내적을 간단하게 구할 수 있게 메서드를 제공한다.
Vector3 vec1 = new Vector3(1,0,0);
Vector3 vec2 = new Vector3(0,1,0);
var dot = VecTor3.Dot(vec1, vec2);
벡터의 외적
벡터의 외적은 3D 벡터에만 해당되는 개념이다. 두 개의 3D 벡터를 입력으로 사용하여, 다른 3D 벡터를 반환한다. 반환하는 벡터는 두 입력 벡터에 대해 수직이다. 오른손 법칙을 사용하여, 입력 벡터의 순서에서 출력 벡터의 방향을 기억할 수 있다. 2개의 벡터가 있을 때 순서를 서로 다르게 하여 벡터의 외적을 구하면 만들어진 두 외적은 서로 정확히 반대 방향을 가리킬 것이다. 벡터의 외적의 크기는, 입력 벡터들의 크기를 곱하고, 그 결과에 두 벡터 사이 각도의 Sin 값을 곱한 것과 같다.
벡터의 외적은 Sin, Cos 같은 함수를 써야할 상황에 외적을 이용하면 최적화에 많은 도움이 된다.