BOJ_1010_다리놓기_JAVA
문제 : 다리놓기
링크 : BOJ_1010_다리놓기
접근 방식
그림과 사례로 설명을 장황하게 했지만 핵심은 조합의 경우의 수를 모두 구하는 문제이다. 하지만 시간복잡도를 따졌을 때 조합 로직을 구현하여 카운트하는 방식으로 하면 시간초과가 난다.
나는 점화식을 통한 DP로 풀었다. 점화식은 다음과 같다.
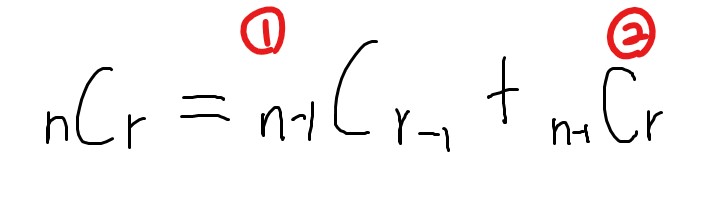
위의 점화식이 나온 배경은 다음과 같다.
- 어떤 특정 원소를 포함시키고 뽑았을 때의 경우의 수
- 특정 원소를 포함시키지 않고 뽑았을 때의 경우의 수
이 두 가지 경우의 수를 합치면 nCr의 경우의 수가 된다.
소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ_1010_다리놓기 {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(in.readLine());
int[][] dp = new int[31][31];
dp[0][0] = 1;
dp[1][0] = 1;
dp[1][1] = 1;
for (int i = 2; i <= 30; i++) {
dp[i][0] = 1;
dp[i][1] = i;
for (int j = 2; j <= i; j++) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
for (int tc = 0; tc < T; tc++) {
StringTokenizer st = new StringTokenizer(in.readLine(), " ");
int m = Integer.parseInt(st.nextToken());
int n = Integer.parseInt(st.nextToken());
// nCm = N! / M! * N-M!;
// nCr = n-1Cr-1 + n-1Cr
System.out.println(dp[n][m]);
}
}
}
풀이 방법
-
line 11 ~ 13 : 테스트 케이스 수를 읽어들여 변수에 저장
-
line 15 ~ 18 : dp 배열을 생성하는데, N과 R의 범위가 30이 최대이므로, 31까지의 배열을 선언해둔다. 이후 초기 설정값을 할당해준다.
-
line 19 ~ 24 : 반복을 돌려 경우의 수를 누적시킨다. 위에 설명한 점화식대로 만드는데, 혹시 몰라서 20, 21라인의 2가지 경우에는 같은 규칙으로 값이 저장되므로 추가해주었다.
-
line 26 ~ 36 : dp배열이 모두 구해졌다면 테스트케이스만큼 반복하여 n, m 값을 읽어들인 후 dp배열의 n,m 번째 값을 출력한다.